お悩み：ケーキを７等分するうまい方法はないでしょうか？

ケーキにしても果物にしても、半分とか４等分、８等分と２の倍数に分けるにはあまり苦労しません。奇数でも３等分ならなんとなくできますので、６等分でもまず半分にしてそれを３等分すれば簡単です。しかし５等分とか７等分となりますとどうしたらいいのかぐっと難しくなります。

私の家は普段は妻と義母との３人暮らしですので、ケーキでも果物でも３等分ですから困るようなことはないのですが、近くに住む娘の家族４人がやってくると７等分しなくてはいけない機会が多くなります。特に高価なケーキとかメロンになりますと子供も大人も真剣に大きさを比べますのできれいに７等分しようといつも苦労してきました。なんとなくこれくらいか、と切り始めますと、途中でなんだかおかしなことになり結果はたいてい不満足です。そこで今回ちょっと腰を据えて、いい方法はないかと考えてみました。

------------------------------------------------------

■アバウトで７等分に近づく
そもそも７等分するといっても工業製品をつくる話ではありませんし、ほぼ７等分であればよいということになりますと発明原理では<#16 アバウト原理> が思い浮かびます。これは、要求仕様を少しだけ緩和したりすると問題が解決することがあるという原理です。今回のケースでは、所詮はケーキや果物を分ける話ですから７等分とはいえ完璧に同じ大きさに分けなくても、人がみてほぼ７等分になっていればよいではないかと考えるわけです。一方で、２の倍数等分とか３等分は悩まずにできるわけですから、このあたりの組み合わせで７等分にうまく近づければよさそうな気がします。

そこでこのように考えてみました。７等分するには、まず８等分してできた８切れの内７個を各人に１つと、残った一切れを７つに分けて各人に加えればよい。つまり
７等分の一切れ　＝　８等分の一切れ　＋　８等分の一切れの７分の１
と考えることができます。

ホールケーキをイメージします。８等分の一切れの大きさは４等分の一切れの半分ですから大きさはイメージできます。その８等分の一切れの大きさはそう大きくありませんので、それを３：４に分けたとして仮にそれらをａ切れ、ｂ切れと呼びましょう。もとのケーキを半分にしたものは８等分の一切れが４個とれる大きさですのでそれにｂ切れを足してできる大きなかたまりを４等分すれば、それは元のケーキを７等分したときの一切れになるはずです。これを「正７分片」と呼びましょう。大きなかたまりを取った残りの小さいかたまりを３等分すればそれはやはり元のケーキを７等分したときの一切れになるはずです。こうすれば全体を正確に７等分できることがわかります。



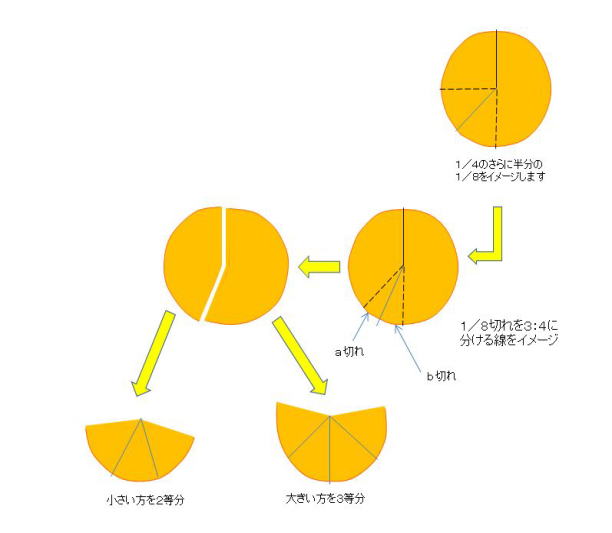
実際に８等分の一切れをほぼ３：４に分けるのであれば、半分よりやや左寄りに分ければよいのですが、「やや」のところが微妙です。もし「半分よりやや左寄りに切る」のと「半分のところを切る」のが、結果的にあまり違いがなければ「半分のところを切る」ほうが簡単です。そこで両者の違いを数字で検証してみました。

丸いケーキ全体の中心角を360°とし、一切れの扇形の大きさを中心角で示します。
上記の「半分のところを切る」方法でつくった大きなかたまりを４等分して出来た一切れを「大概７分片」と呼ぶことにしますと次の数字がでてきます。

１） 正７分片の中心角＝ 360°( 1/7 )　＝　51.4°
２） 大概７分片の中心角＝ 360°( 1/2 + 1/16 )÷4 ＝ 50.6°

大きなかたまりを切り取ったあとの小さなかたまりを３等分したものを「小概７分片」と呼ぶことにしますと中心角はつぎの数字になります。

３）小概７分片の中心角＝ 360°( 1/2−1/16 )÷3 ＝ 52.5°

大概７分片も小概７分片も正７分片に近く、「大概７分片」と「小概７分片」の中心角の違いも2.1°ですから全体の中心角360°の１パーセント未満です。ケーキそのものがクリームやチョコレートの付き具合など均一ではありませんので、ナイフで切る場合の中心角の1パーセント未満の多寡は誤差の範囲と考えてよいでしょう。つまり、実用的には十分に七等分できていることが分かりました。上記の式２）３）で表される切り方を[７等分手順]と呼ぶことにします。

[７等分手順]の大きいかたまりの中心角＝360°( 1/2 +1/16 )＝202.5°

と正７分片４個分の中心角205.7°との差は3.2°です。これは、直径20cmのケーキの外側において5.6mmの違いになります。直径30cmのケーキでは8.4mmです。従いまして、大きなかたまりと小さなかたまりを切り分けるとき[７等分手順]なら、僅かに（直径20cmのケーキなら外側で5mm程度）左寄りに切ればより正確な7等分ができることになります。

以上まとめますと、発明原理<#16 アバウト原理>　による７等分方法はつぎの図で示すものになります。




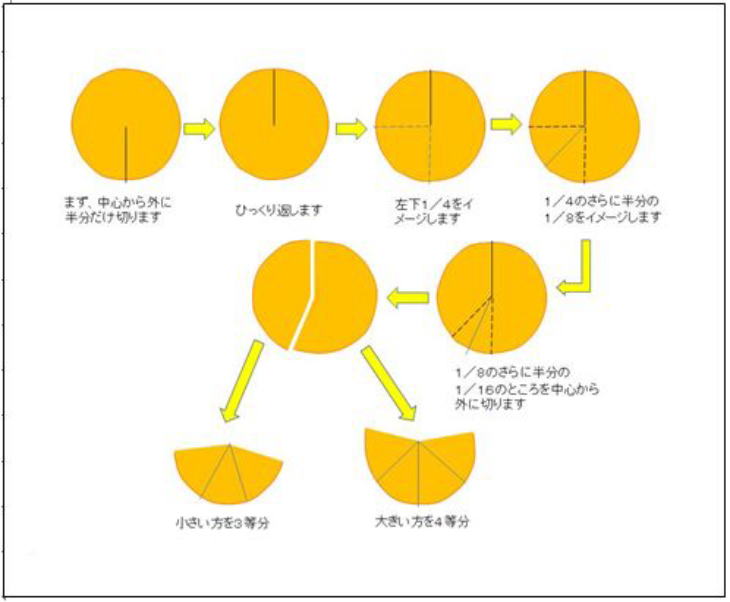
手順を書きますと、

[７等分手順]
（１） 中心から外に半分だけ切ります
（２） ぐるりと180°まわして、切れ目を向こう側にします
（３） 切れ目を通る中心線から左下の四半分をイメージします
（４） 左下四半分をさらに半分にした２つの扇形をイメージします
（５） そのうち右側の扇形の中央線をイメージし、それに沿って中心から外に切ります
このようにして大きいかたまりと小さいかたまりができます
（６） 大きいかたまりを半分にし、それらをさらに半分にすると4つの大概７分片ができます
（７） 小さいかたまりを３等分すると３つの小概７分片ができます

次の写真は、オレンジ色の紙の円をケーキに見立てて[７等分手順]に忠実に沿って切ってみたものです。いかがでしょうか。




目視する限りほぼ正確に７等分されているように見えますのでこれで十分と思いますが、手順（５）で切るとき、ほんの僅か（直径20cmのケーキの場合で5mm程度）左寄りに切れば、より正確な7等分ができるはずです。（７）で３等分するときは、（６）でできた一切れの大きさと同じ大きさの一切れを切り取り、残りを２等分すれば簡単です。

私の家にはこれからも娘家族がしばしばやってくるでしょうから、ケーキでなくてもリンゴや柿、梨やメロンを７等分するのが楽しみです。


■５等分にも
ここまで来ますと５等分の切り方も考えてみたくなります。
やはり<#16 アバウト原理>ですが、７等分の方法の過程でできる大きなかたまりと小さなかたまりを眺めていますとそのまま５等分するのにも使えそうな気がします。実際に大きなかたまりと小さなかたまりそれぞれを３等分と２等分してみますと、結構似た大きさになることがわかります。では数値的にどうなるのか検証してみましょう。

正確に５等分した一切れを「正５分片」、大きなかたまりを３等分して出来た一切れを「大概５分片」と呼ぶことにしますと次の数字がでてきます。

１） 正５分片の中心角＝ 360°( 1/5 )　＝　72.0°
２）大概５分片の中心角＝ 360°( 1/2 + 1/16 )÷3 ＝ 67.5°
大きなかたまりを切り取ったあとの小さなかたまりを３等分したものを「小概５分片」と呼ぶことにしますと
３）小概５分片の中心角＝ 360°( 1/2−1/16 )÷2 ＝ 78.8°

となり、大概５分片と小概５分片の中心角差が11.3°になります。これは全体360°の3パーセント(0.0313)ですのでこれも誤差の範囲と考えられなくはないでしょうが、[７等分手順]の誤差よりやや大きいので、もう少し誤差少なくする切り方を考えてみましょう。

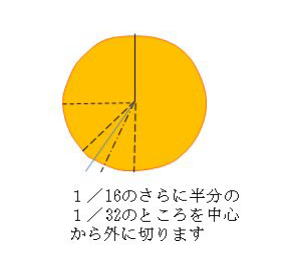
上記２）と３）の式を見てみますと、大概５分片の中心角がやや小さく、小概５分片の中心角やや大きいことがわかります。そこでこれらに1/32の調整をしますとつぎのようになります。
２‘）大概５分片の中心角＝ 360°( 1/2 + 1/16+1/32 )÷3 ＝ 71.3°
３‘）小概５分片の中心角＝ 360°( 1/2−1/16−1/32 )÷2 ＝ 73.1°
これによりますと、正５分片との中心角の差は、1°くらいで、大概５分片と小概５分片の差も2°未満という申し分ない分け方になります。
これは[７等分手順]の（５）を次のように変えたものになります

（５‘）その扇形のさらに半分の２つの扇形をイメージし、そのうち左側の扇形の中央線に沿って中心から外に半分切ります。

これを示したのが次の図です。




全体の手順は以下です。




手順を書きますと以下のようになります。
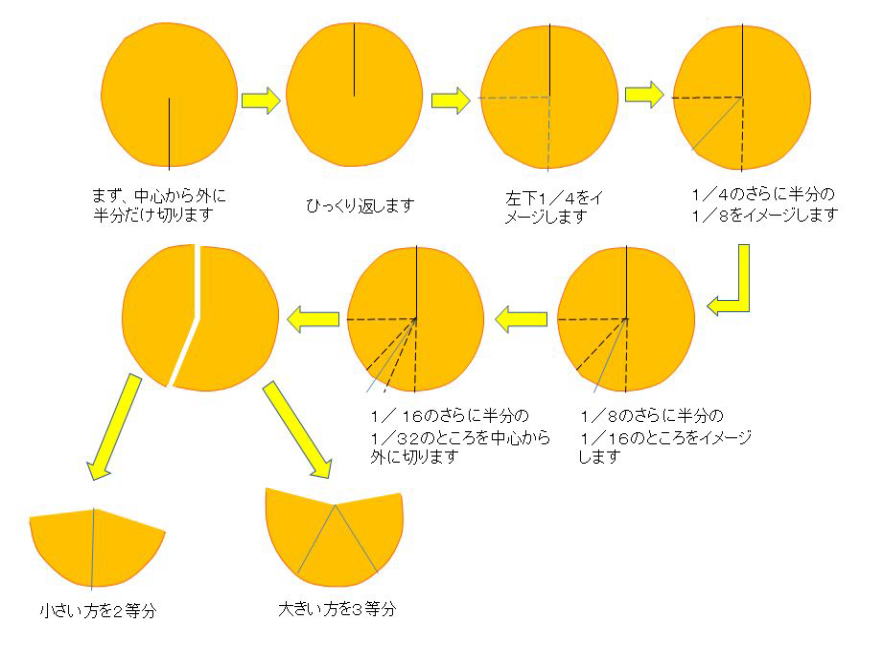
[５等分手順]
（１） 中心から外に半分だけ切ります
（２） ぐるりと180°まわして、切れ目を向こう側にします
（３） 切れ目を通る中心線から左下の四半分をイメージします
（４） 左下四半分をさらに半分にした２つの扇形をイメージします
（５） そのうちの右側の扇形をさらに半分にした２つの扇形をイメージします
（６）　そのうちの左側の扇形の中央線をイメージし、
それに沿って中心から外に切ります
このようにして小さいかたまりと大きいかたまりができます
（７） 小さいかたまりを半分にすると２つの小概５分片ができます
（８） 大きいかたまりを３等分すると３つの大概５分片ができます

小さなかたまりを２等分する方を先に書いたのには理由があります。
それは２等分する方がやりやすいからです。小さなかたまりの２等分をつくれば、小概５分片が２つできますので、大きなかたまりを３等分するときには小概５分片にあわせて一つ切り出し、残りを２等分すれば簡単です。


[５等分手順]の大きいかたまりの中心角
360°( 1/2 +1/16 +1/32 )＝213.8°
と正５分片３個分の中心角216.0°の違いは2.2°です。これは、直径20cmのケーキですと外側において3.8mmの違いになります。直径30cmのケーキでは5.8mmです。従いまして、大きなかたまりと小さなかたまりを切り分けるとき[５等分手順]でも、僅かに（直径20cmのケーキなら外側で4mm程度）左寄りに切ればより正確な５等分ができることになります

次の写真は、オレンジ色の紙の円をケーキに見立てて[５等分手順]に忠実に沿って切ってみたものです。




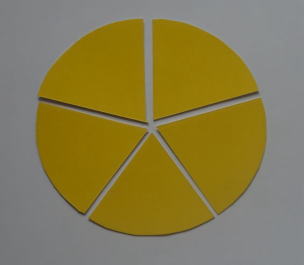
いかがでしょうか。目視する限りほぼ正確に５等分されているように見えますのでこれで十分と思いますが、手順（６）で切るとき、ほんの僅か（直径20cmのケーキの場合で4mm程度）左寄りに切れば、より正確な５等分ができるはずです。（８）で３等分するときは、（７）でできた一切れの大きさと同じ大きさの一切れを切り取り、残りを２等分すれば簡単です。


■まとめ
以上、連載第10回でご紹介しましたことをまとめますと以下になります。

■ケーキを７等分するには発明原理の<#16 アバウト原理>を適用して、半分あるいは四半分をイメージすることを組み合わせた、つぎの手順で可能です。
[７等分手順]
（１）中心から外に半分だけ切ります
（２） ぐるりと180°まわして、切れ目を向こう側にします
（３） 切れ目を通る中心線から左下の四半分をイメージします
（４） 左下四半分をさらに半分にした２つの扇形をイメージします
（５） そのうち右側の扇形の中央線をイメージし、それに沿って中心から外に切ります
このようにして大きいかたまりと小さいかたまりができます
（６） 大きいかたまりを半分にし、それらをさらに半分にすると４つの７分片ができます
（７） 小さいかたまりを３等分すると３つの７分片ができます


■ケーキを５等分するには、つぎの手順で切ります。
[５等分手順]
（１）〜（４）は[７等分手順]と同じ
（５） 右側の扇形をさらに半分にした２つの扇形をイメージします
（６）　そのうちの左側の扇形の中央線をイメージし、
それに沿って中心から外に切ります
このようにして小さいかたまりと大きいかたまりができます
（７） 小さいかたまりを半分にすると２つの小概５分片ができます
（８） 大きいかたまりを３等分すると３つの大概５分片ができます


上記７等分手順、５等分手順いずれにおいても、小さいかたまりと大きいかたまりに切り分けるとき、大きいかたまりがほんの僅か（注）に大きくなるように切れば、より正確な等分ができます。
注：直径20cmのケーキの場合、外側で5mm程度